√70以上 場合の数 小学生 公式 331894
Web予約においてお子様 幼児の入力をすると部屋在庫が出て来ない場合の対処方法 香住佐津温泉 民宿 美味し宿かどや公式ブログ
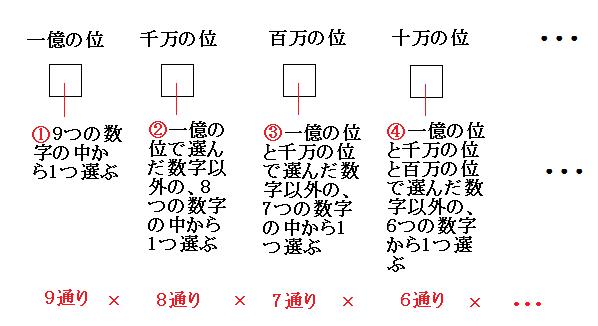
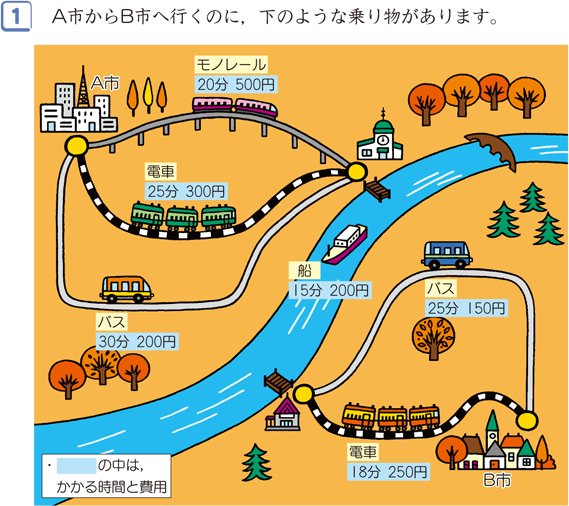
公式を使う場合は、聞かれている数の 単位 をよく見る ことが大切です。 この問題では「何m」ですから、公式のうち「道のり」の式を使えば良い、と分かります。 公式は ① 道のり (m)=間かく(mおき)×間の数(個) なので、このことから場合の数と確率は非常に似ていることがわかります. そのため 確率を極めたければ,場合の数を極めるべし! では場合の数について見ていきましょう. 場合の数はどうやって求めるの? 条件に合うものを 書きだすのも1つの手 です
場合の数 小学生 公式
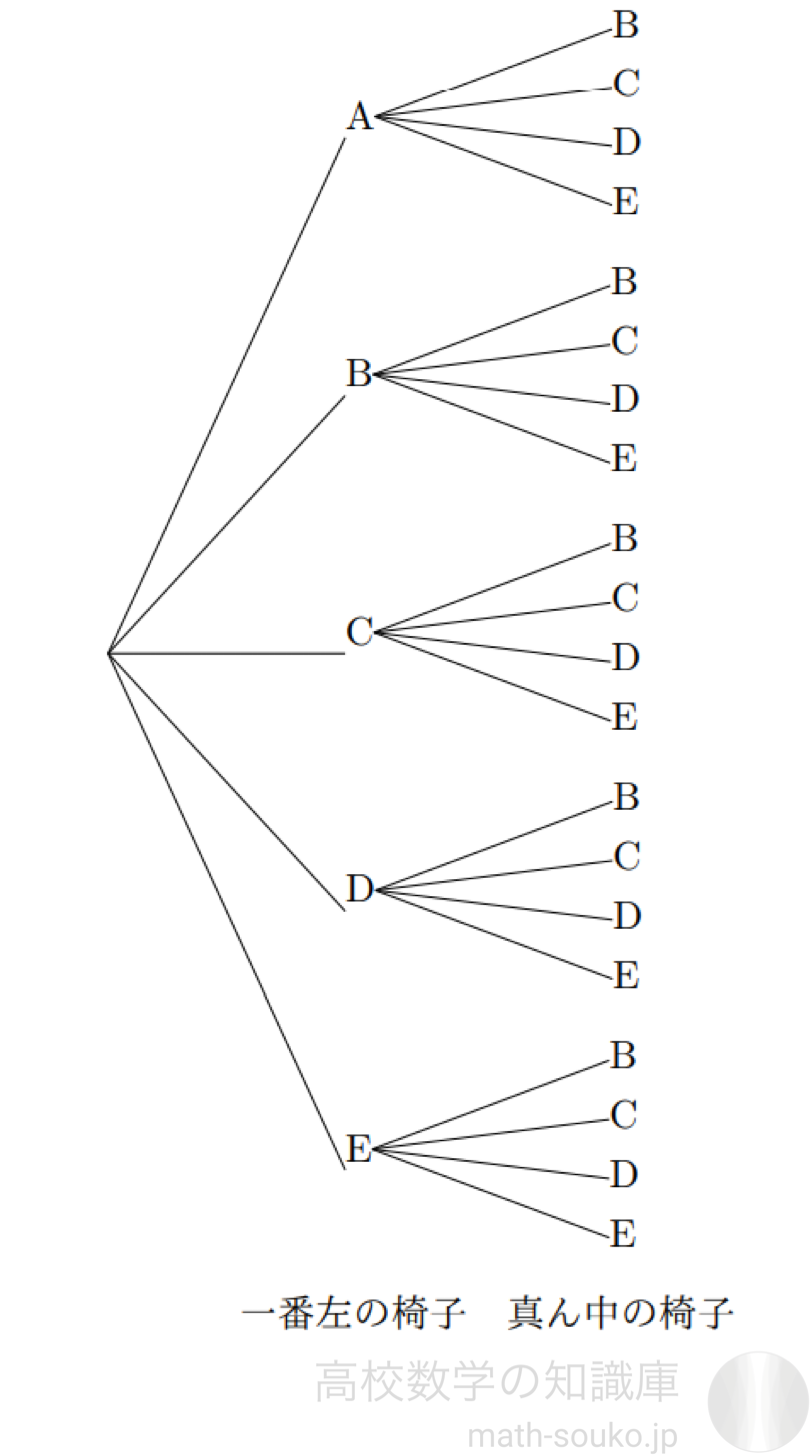
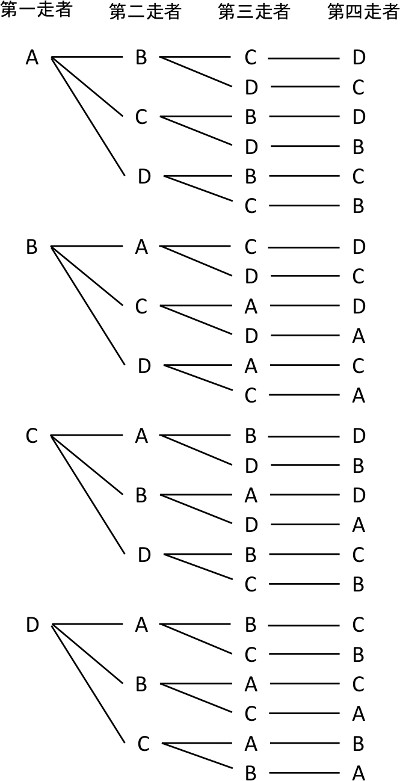
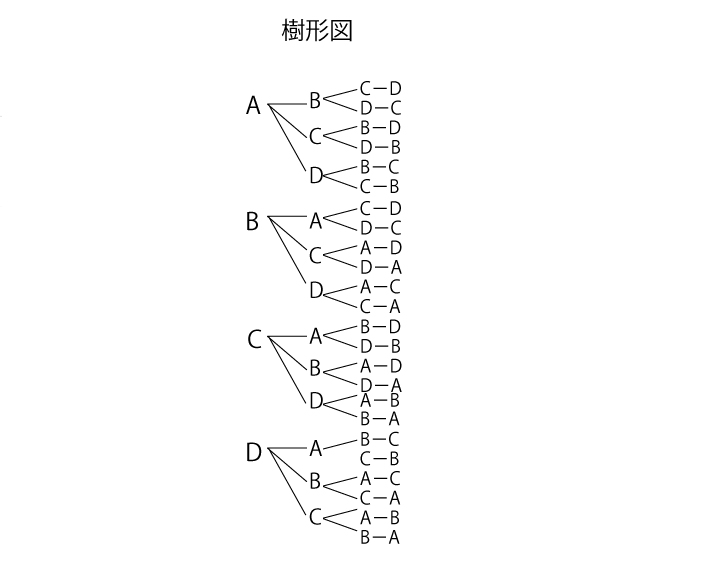
場合の数 小学生 公式- こんにちは。 da Vinch (@mathsouko_vinch)です。 場合の数を数える皆さんは次のような問題を解くときどのように考えますか。3人の人が、3つの横に並べられた椅子に座る座り方は何通りあるか。 例えば小学生なら、問題の意出た目の数だけ進み、これを何度も繰り返します。 (1)サイコロを2回振って、aにくる目の出方は何通りありますか。 (2)サイコロを3回振って、aにくる目の出方は何通りありますか。 (3)サイコロを5回振って、2回目も5回目もaにくる目の出方は 何通りあります

算数 場合の数の解き方は 問題別に考え方を解説 数スタ
日本大百科全書(ニッポニカ) 場合の数の用語解説 いくつかの事柄について「全部で何通りの場合があるか」数え上げるような問題を「場合の数」を求める問題とよんでいる。この種の問題において基礎となるのは次の二つの法則である。植竹恒男和の法則二つの事柄a、bがあって、おのおの 小学校で扱う場合の数の組み合わせの考え方 順列 (並べ方)とはまた違った数え方をしないといけない組み合わせ。 うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。 今回の記事では、組み合わせの数の数え方について こんにちは、ももやまです。 今回は、 中学入試 高校入試 共通テスト(大学入試) spi(就職試験) 基本情報 など、様々な場面で出てくる場合の数、特に「順列と組み合わせの違い」に注目して説明していき
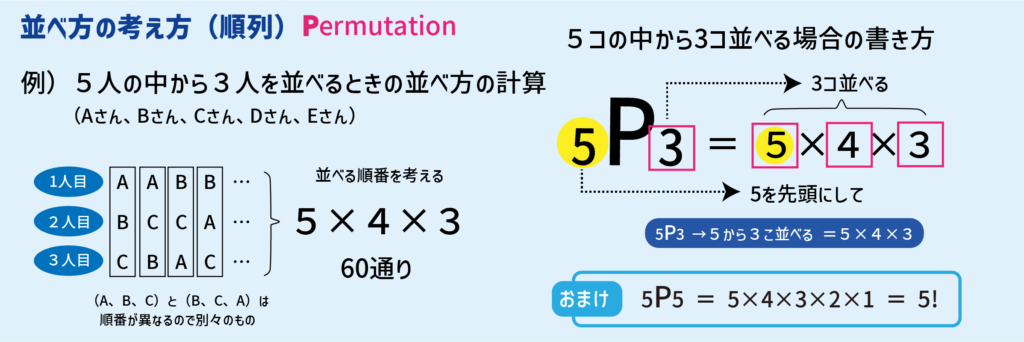
一連の記事はこちら 場合の数1|和の法則と積の法則は超アタリマエ! 場合の数2|順列のnPrの考え方と公式は超カンタン! ←今の記事 場合の数3|実はカンタンな円順列と数珠順列の考え方 場合の数4|組み合わせのnCrの求め方から性質まで攻略割合の3つの公式の覚え方と使い方|小学生に教えるための分かりやすい説明 管理人 10月 11, 18 / 10月 31, 18 得意な子は公式をわざわざ覚えなくても感覚で文章問題を解いてしまいます。一連の記事はこちら 場合の数1|和の法則と積の法則は超アタリマエ! ←今の記事 場合の数2|順列のnPrの考え方と公式は超カンタン! 場合の数3|実はカンタンな円順列と数珠順列の考え方 場合の数4|組み合わせのnCrの求め方から性質まで攻略
場合の数 小学生 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 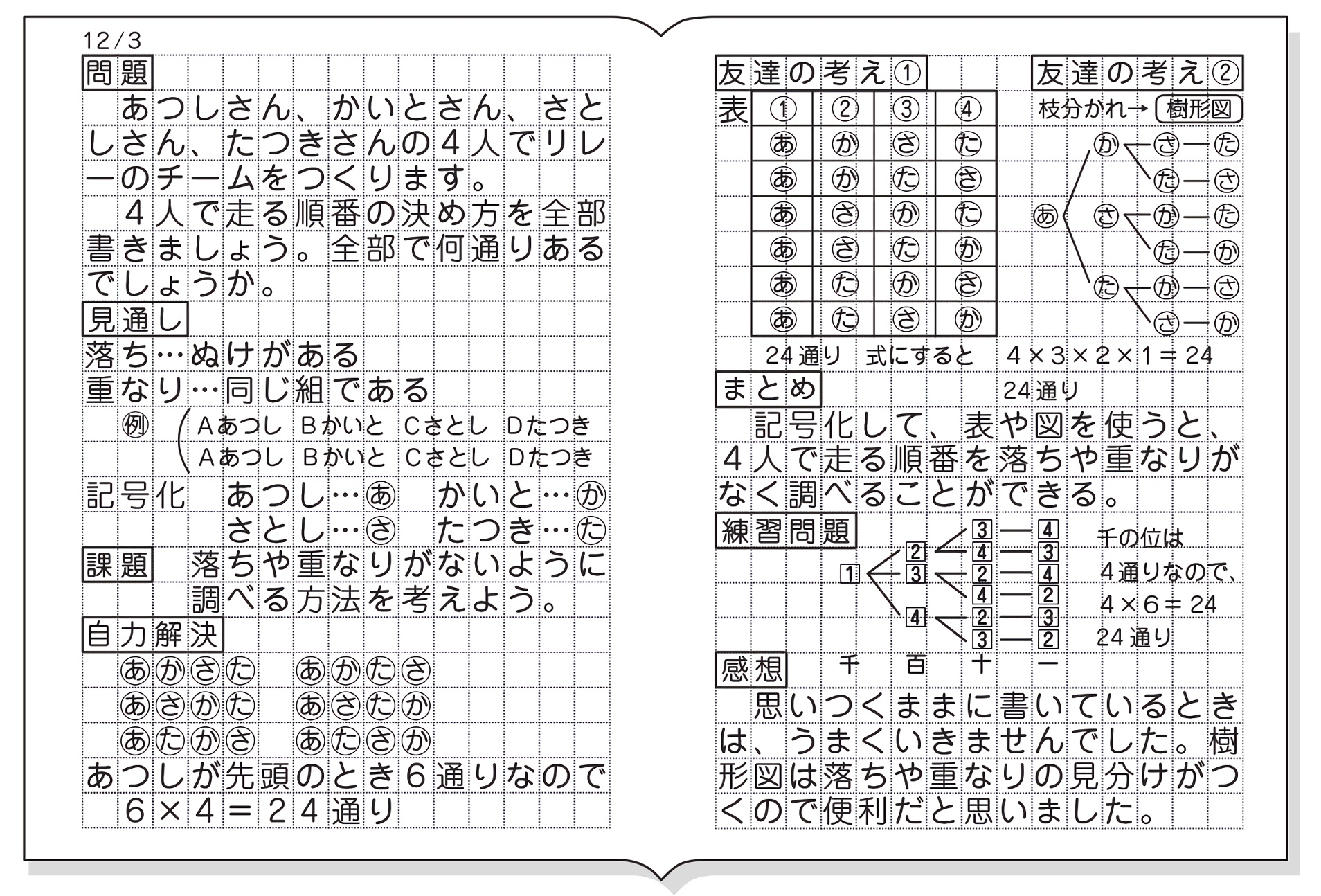 |  |
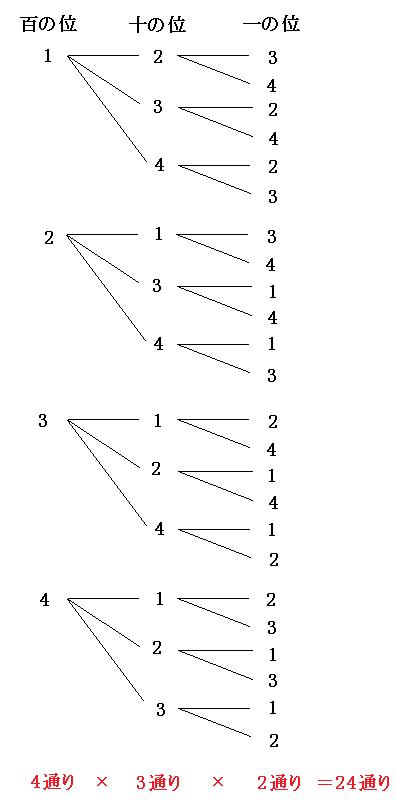 |  | 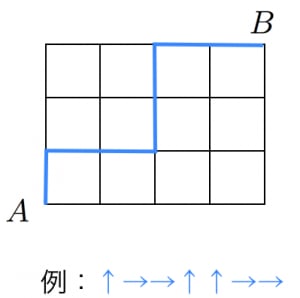 |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 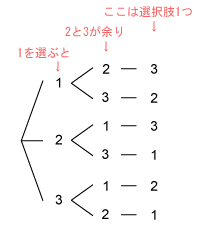 |  |
 |  |  |
 |  | |
「場合の数 小学生 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
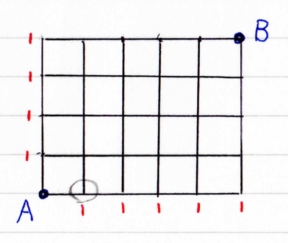
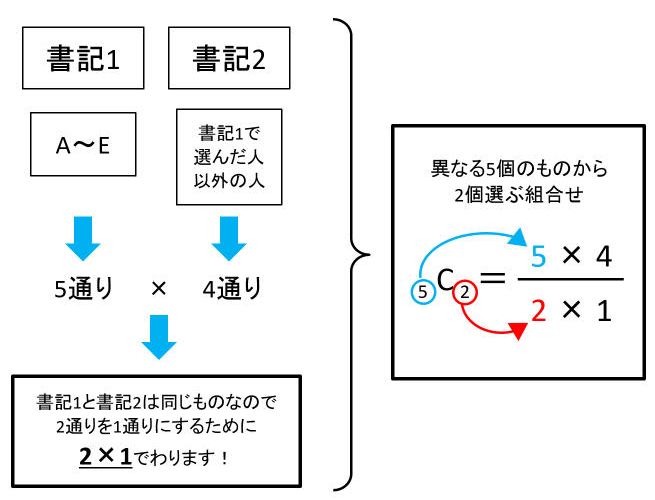
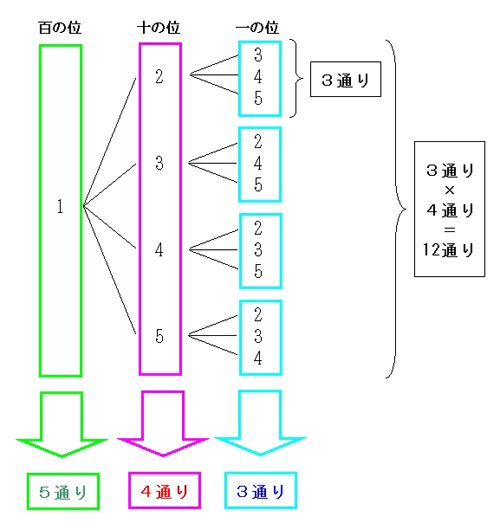
重複組み合わせの公式がどのようにして得られるのかを紹介しておきます。 「\(n\) 種類のものから重複を許して \(r\) 個選ぶ方法」は、「\(r\) 個のモノと \((n − 1)\) 個の仕切りを一列に並べる方法」と同じ場合の数になります。しかし、この問題も、数ある頂点の中から4つの頂点を選ぶ問題だと思えば、場合の数の学習が応用できる。 横には4つの頂点が並んでいる。 4つの頂点から2つの頂点を選ぶと、横の辺が決まる。 同じように、 縦には5つの頂点が並んでいる。
コメント
コメントを投稿